07.11.2022.

Ar apzīmējumu jauno mediju māksla saprot tādus mākslas darbus, kas izstrādāti izmantojot  multivides tehnoloģijas. Viens no jauno mediju mākslas apakšveidiem ir fraktāļu māksla, kura radās 80. gadu vidū. Par fraktāļu ģeometrijas radītāju un nosaukuma izgudrotāju galvenokārt tiek uzskatīts Polijā dzimušais ebreju izcelsmes franču/amerikāņu matemātiķis Benuā Mandelbrots (Benoit Mandelbrot, 1924-2010).
Mandelbrots 70. gados uzsāka pētīt matemātiskus modeļus, kurus bija izveidojis franču matemātiķis Gastons Moriss Džūlija (Gaston Maurice Julia, 1893-1978) un kuri bija pazīstami ar nosaukumu Džūlija kopas (Julia sets). Benuā Mandelbrots kopš 1958. gada strādāja datoru tehnoloģiju korporācijā IBM un šajā uzņēmumā viņam bija piekļuve jaudīgām datortehnoloģijām, kas jau bija spējīgas apstrādāt šādu informāciju. Apstrādājot Džūlija kopas ar datora palīdzību un iepazīstot to topoloģiju, viņš 1979. gadā izveidoja pats savu Mandelbrota kopu, kas sastāvēja no dažādu Jūlija kopu apvienojuma. Mandelbrota kopā katrs tās punkts (vai koordināta) atbilda Jūlija fraktālim matemātiskā vidē. Funkcijas grafisku attēlojumu varēja iegūt, ja pikselim ar koordinātām x, y piešķīra krāsu, atbilstoši veikto iterāciju skaitam. Gadījumā, ja šis skaitlis izgāja ārpus orbītas robežām, tam atbilstošais pikselis tika iekrāsots baltā krāsā.

1.Piemērs ar Jūlija kopu. Foto: http://prism.troy.edu/adickinson/fractalGroup/index.html

2. Piemērs ar Mandelbrota kopu. Foto: http://prism.troy.edu/adickinson/fractalGroup/index.html

Ģeometriskās formas, kuras veidoja attēlu Mandelbrots nosauca par fraktāļiem. Vārds fraktālis ir atvasināts no latīņu fractus. Darbības vārds frangere nozīmē salauzt; radīt neregulārus fragmentus. Un tāpēc, ka šis vārds vienlaikus apzīmēja gan fragmentu, gan neregularitāti apzīmējums Mandelbrotam šķita ļoti piemērots sava atklājuma nosaukšanai. Vienkāršā valodā runājot, fraktālis ir ģeometriska forma, kura atkārtojas gan lielākā, gan mazākā mērogā un vienalga cik ļoti tā tiek pietuvināta, tā nekļūst vienkāršāka. Dabā viegli novērojams piemērs ir krasta līnija, kuras robojums atkārtojas neatkarīgi vai uz to lūkojas no kosmosa vai sev pie kājām. Mandelbrots viens no pirmajiem parādīja kā vizuāli sarežģīts veidojums var tikt radīts izmantojot vienkāršas likumsakarības. Izrādījās, ka dabas objekti, kurus cilvēki bija ieraduši uzskatīt par haotiskiem vai nekonkrētiem kā mākoņi, koku lapotnes, krasta vai kalnu apveidi, patiesībā veidojas pēc noteiktas kārtības. Fraktāļi bija tas trūkstošais posms, kurš palīdzēja savienot tīro matemātiku ar dabaszinātnēm. Fraktāļu ģeometrija, kas sastāv no daudzām kopām (ne tikai Džūlija vai Mandelbrota atrastajām) šodien palīdz grafiski modelēt dabas fenomenus zinātniskiem pētījumiem, piemēram veidot augu augšanas simulācijas, apvidus reljefu un jūras virsmu modeļus, gan arī izveidot dažādus mākslas objektus. Fraktāļiem ir būtiska loma datorgrafikā.  Mūsdienās ar fraktāļu palīdzību ir iespējams attēlot gandrīz jebkuru dabā atrodamo objektu. Nepieciešams tikai atrast īsto formulu un iterācijas procesa metodi.
Daudzi fraktāļu mākslas paraugi atstāj patīkamu saskanīguma un harmoniskuma iespaidu, kuru panāk ar tādu modeļu palīdzību, kuros izlīdzsvaroti kārtības un haosa elementi. Līdzīgi principi ir aprakstīti ķīniešu glezniecībā un dārzu iekārtojumā. Mainot krāsas izvēles algoritmu, ir iespējams iegūt daudzveidīgus krāsainus fraktāļa attēlus ar atšķirīgiem zīmējumiem.
1982. gadā Mandelbrots publicēja savas grāmatas “Dabas fraktāļu ģeometrija” 3. izdevumu, kas bija populārzinātniskāks par iepriekšējiem un veicināja fraktāļu popularitāti plašākā auditorijā. Fraktāļu ilustrācijas pirmoreiz tika izrādītas izstādē “Haosa skaistums” Minhenē (1985) un tajā pašā gadā Ņujorkā ar nosaukumu “Haosa celmlauži”. To bija veidojuši vācu matemātiķi Heincs Otto Peitgens (Heinz-Otto Peitgen) un Pēters H. Rihters (Peter H. Richter), kuri vēlāk publicēja grāmatu ar nosaukumu “Fraktāļu skaistums” (1986).  Abu zinātnieku mākslinieciskās ambīcijas tika apšaubītas, tobrīd fraktāļi netika atzīti par mākslu, jo pēc kritiķu domām darbiem trūka izvēles brīvības un cilvēcisku šaubu elementa. Uz šo kritiku viņi atbildēja citējot Pikaso “Māksla ir meli, kuri ļauj mums atpazīt patiesību” un piebilstot, ka “varbūt tā arī nav dziļa patiesība atklāt, ka mūsu pasaule ir nelineāra un sarežģīta. Mūsu ikdienas pieredze nekad nav apliecinājusi pretējo. Tomēr fizika, matemātika un citas zinātnes līdz šim bija lieliski ignorējušas acīmredzamo. Fiziķiem tas bija pārsteigums, ka pat viņu vienkāršākajos vienādojumos ir klātesošs haosa elements.”
Izstāde apceļoja 40 valstis un piesaistīja arvien lielāku uzmanību. Laikmetīgās mākslas jaunais muzejs Ņujorkā 1989. gadā nolēma organizēt izstādi ar nosaukumu “Dīvainie uzmanības piesaistītāji: Haosa zīmes” kuras galvenais vēstījums bija, ka šķietamajam haosam piemīt sava loģika.

3. Stīvs Millers, Pakāpeniska un labprātīga pielāgošanās, 1988, no izstādes “Dīvainie uzmanības piesaistītāji: Haosa zīmes”, 1989. Foto: https://archive.newmuseum.org/print-ephemera/6467

No matemātikas viedokļa fraktāļus iedala algebriskajos, ģeometriskajos un stohastiskajos, taču no estētiskā aspekta aprēķināšanas veidiem nav tik lielas nozīmes, tāpēc varam vienkārši runāt par abstrakto mākslu - vienkāršāku vai sarežģītāku formu fraktāļiem. Vissarežģītākie ir stohastiskie fraktāļi, kuri ir līdzīgi jau pieminētajiem dabas veidojumiem -  kokiem, robotām krasta līnijām, liesmām utt.

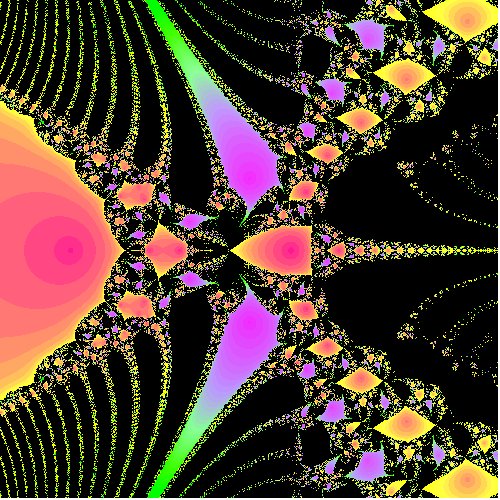
4. Algebriskais fraktālis, Ņūtona baseina piemērs. Foto:  https://www.unf.edu/~ddreibel/teaching/newton/aditya2.jpg

5. Ģeometriskais fraktālis, Koha sniegpārsliņas piemērs. Foto: https://upload.wikimedia.org/wikipedia/commons/3/3f/Koch_snowflake_%28RGB-CMY%29.jpg

6.Stohastiskais fraktālis, Brauna koka piemērs. Foto: https://library.fridoverweij.com/codelab/brownian_tree/brownian_tree_center_up.html (linkā iespējams aplūkot arī “augšanas” procesu

Stohastiskais fraktālis Brauna koks nosaukts angļu biologa Roberta Brauna vārdā (tā paša, kura vārdā nosaukta Brauna kustība, kuru šis zinātnieks fiksēja 1827. gadā) Brauna koks plašākā sabiedrībā kļuva populārs 1990. gados, kad personālajiem datoriem parādījās pietiekami liela jauda, lai simulētu Brauna daļiņu haotisko kustību.
Amerikāņu matemātiķis Skots Dravess (Scott Draves) 1992. gadā paplašināja fraktāļu funkciju klasi ar jaunu fraktāļu tipu – liesmu fraktāļiem. 1993. gadā viņš vienu no saviem fraktāļiem ar nosaukumu “Liesma #149” iesniedza Austrijā dibinātajai datorgrafikas, animācijas un mūzikas balvai Prix Ars Electronica balvai, kas ļāva šiem fraktāļiem tāpat kā māksliniekam iegūt plašāku atpazīstamību.

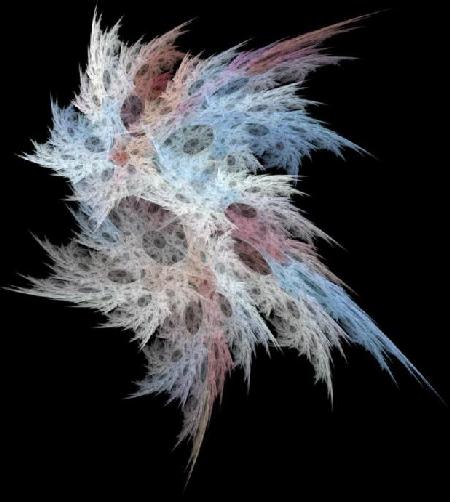
7. Skots Dravess, Liesma #149, 1993. Foto: http://people.math.binghamton.edu/alex/

Liesmu ģenerēšanas programmatūra pēc Dravesa atklājuma bija brīvi pieejama un to sāka plaši izmantot. Viens no šādiem lietotājiem bija mākslinieks Rodžers Džonstons (Roger Johnston), kurš tiek uzskatīts par vienu no talantīgākajiem liesmu fraktāļu veidotājiem, pateicoties to smalkajām detaļām un bagātīgajām krāsām.

8. Rodžers Džonstons, Fraktālis-2, 2000ie gadi. Foto: https://mtmuchmore.files.wordpress.com/2013/03/fractal-2.jpg

Savdabīgu Mandelbrota kopas fraktāļu apstrādes veidu 1993. gadā izveidoja matemātiķe Melinda Grīna (Melinda Green). Viņas veidotie fraktāļi atgādināja sēdošu Budas figūru. Māksliniece tos nosauca par Budabrotiem.

9. Melinda Grīna, Budabrots 20000, 1993. Foto: https://upload.wikimedia.org/wikipedia/commons/9/9c/Buddhabrot_20000.png

NASA inženiere Kerija Mičela (Kerry Mitchell) darbā “Siltais mirdzums” Budabrotu padara līdzīgus liesmojošai dabas parādībai.

10. Kerija Mičela,Siltais mirdzums, 2003. Foto:  https://www.ultrafractal.com/showcase/kerry/warmglow.html

Fraktāļi var tikt attēloti ne tikai divās, bet arī trijās dimensijās. Trīsdimensiju fraktāļus 1997. gadā pirmo reizi konstruēja holandiešu dizaineris Žils Ruiss (Jules Ruis) un 2009. gadā tālāk izstrādāja Daniels Vaits (Daniel White) un Pols Nīlanders (Paul Nylander), izmantojot sfēriskas koordinātes un fraktāli nosaucot par “Mandelbulb”.

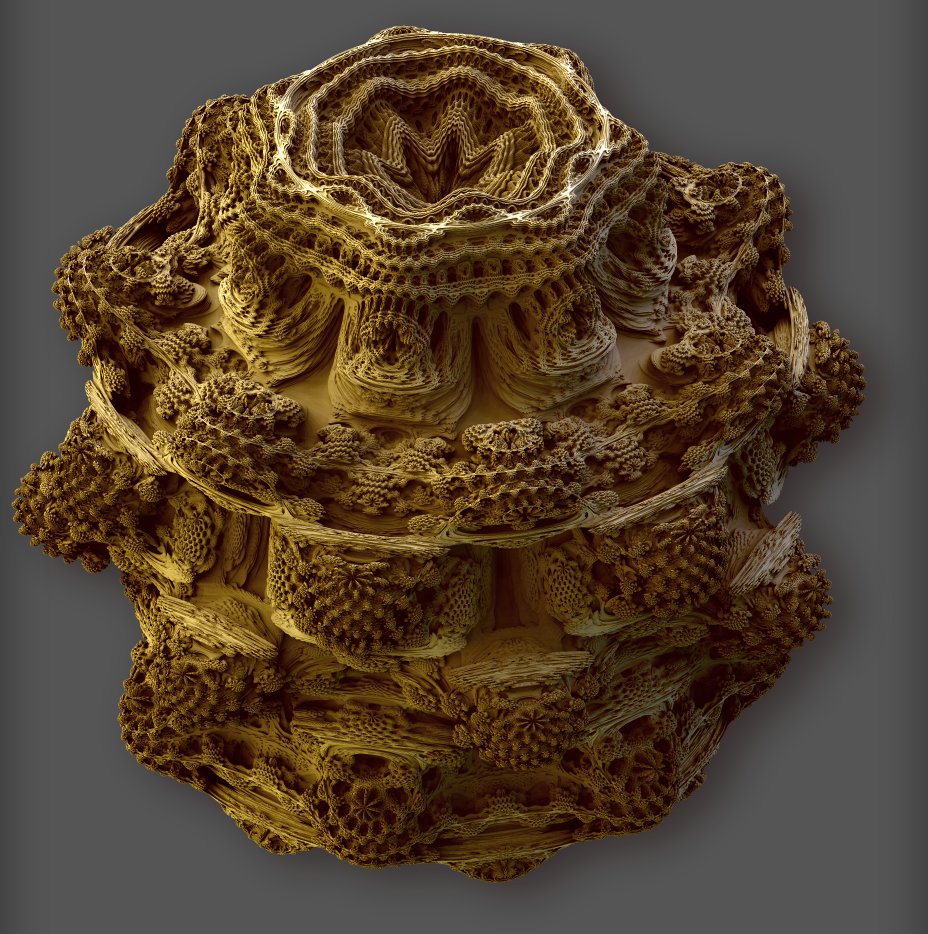
11. Daniels Vaits, Mandelbulbs, trīsdimensiju fraktālis 2009. Foto: https://www.skytopia.com/project/fractal/mandelbulb.html

Lai arī diskusijas par mākslīgā intelekta ģenerētas un aprēķinātas mākslas “īstumu” joprojām ir sastopamas (atcerēsimies, ka arī fotomākslas pirmsākumos tika apšaubīta tās mākslinieciskā potenciāla iespējamība), fraktāļu mākslinieki tālab neuzskata sevi par mazāk radošiem. Britu mākslinieks Viljams Lathams (William Latham), runājot par mākslas darbu veidošanos ar fraktāļu formu atlases palīdzību, norāda uz pilnīgi cilvēciskas izvēles un tēlu veidošanas klātbūtni: “Šo matemātisko variāciju vērošana ir līdzīga psiholoģiskas ainavas izpētei. Es vienmēr izvēlējos to, kas izskatījās nedaudz pēc rokoko, nedaudz pēc baroka, kaut ko no Hansa Rūdolfa Gīgera darbiem. Mana estētiskā izjūta noteica tēlu evolūciju. Mani uzrunāja līdzības ar grieķu bruņucepurēm, ķirbjiem, vīrusiem, lāsveida ornamentiem.”
Kalifornietis Jakobs Anknijs (Jacob Ankney) savus fraktāļus transformē ziedos, kokos un citos augu motīvos ar bagātīgu tekstūru un plūstošām krāsu pārejām.

12. Jakobs Anknijs, Manhetenas projekts, 2010. Foto: https://www.deviantart.com/jeddaka/art/The-Manhattan-Project-145889426

Amerikāņu inženieris Pauls Decelle (Paul DeCelle) izmanto Mandelbrota kopas variantu un piešķir tai gliemežvākam līdzīgu perlamutra nokrāsu un izteiksmīgāku reljefu ar ēnu palīdzību.

13. Pauls Decelle, Dziesma uz bis, 2006. Foto: http://photos1.blogger.com/blogger/2414/257/1600/fract2.0.jpg

Britu māksliniece Tīna Olojede (Tina Oloyede) darbojas kopš 1999. gada un fraktāļu mākslu apguvusi pašmācības ceļā. Viņa izmanto programmu Ultra Fractal, kas datubāzē apkopojusi tūkstošiem fraktāļu tipu, kurus var izmantot tālākai apstrādei. Savos darbos viņa tiecas radītajām vizuālajām formām piešķirt papildus nozīmes. Māksliniece uzskata, ka fraktāļi nav tikai abstrakti dekoratīvi ornamenti un tiem, gluži tāpat kā citu žanru mākslas objektiem, iespējams piešķirt arī dziļāku jēgu un skaidru vēstījumu.

14. Tīna Olojede, Neglītais pīlēns, 2007. Foto: https://aartika.com/art-of-infinity-fractal-art-exhibition-2007

15. Tīna Olojede, Grebums, 2015. Foto: https://aartika.com/icm-fractal-art-exhibition

Fraktāļi var tikt veidoti ne tikai kā atsevišķi attēli, bet arī iekļauti video formātā, tādejādi vēl vairāk sapludinot robežas starp datoranimāciju un fraktāļu mākslu. Nīderlandiešu fraktāļu mākslinieka Jūlija Horsthuisa (Julius Horsthuis), filma “Fraktāļu laiks” aizved mūs neierastā atsvešinātā un kosmiskā abstraktās mākslas piedzīvojumā. Viņa filmu žurnāls “Forbes” atzina par vienu no 35 labākajām paplašinātās realitātes jeb extended reality pieredzēm 2019. gadā. 

Šāda realitātes paplašināšana ļauj mums šķietami nokļūt citā pasaulē pat nepieceļoties no krēsla. Un kādiem no mums tas ļauj aizdomāties par to vai tēliem skaistumu piešķir tikai izmantoto formu sarežģītība un harmoniskums, vai tur tomēr jāmeklē vairāk, kādas norādes uz dzīvību šajā kosmosā.

Autore : Krista Balode

Izmantotā literatūra:
1. Fractal Art: Beaty and Mathematics // Congreso Internacional de Matematicos. Madrid: Graficas Almudena SL – 2006.
2. Lynn Gamwell, Mathematics and Art: A Cultural History. – New Jersey: Princeton University Press, 2015.
3. The Science of Fractal Images // Ed. By Heinz-Otto Peitgen and Dietmar Saupe – New York: Springer-Verlag, 1988
4. Wolfram Stephen, The Father of Fractals // Wall Street Journal, 22.11.2012.
5. https://www.scientificamerican.com/article/mandelbrot-set-1990-horgan/
6. https://www.artechouse.com/fractal-art-with-artist-julius-horsthuis/
7. http://www.julius-horsthuis.com/
8. https://www.hisour.com/fractal-art-17953/
9. https://www.desmondhenry.com/
10. https://www.gold.ac.uk/news/the-art-of-william-latham/
11. https://www.psu.edu/news/research/story/fractal-dances-nature/
12. http://www.kerrymitchellart.com/tutorials/buddhabrot2/buddhabrot2-tutorial.html
13. https://superliminal.com/fractals/bbrot/
14. https://www.aartika.co.uk/index.php/portfolio/tina-oloyede-artist-biography